
A common situation that any data scientist may come across: You have two sets of observations, and you want to test whether they are drawn from the same distribution.
For example, you measure the masses of a bunch of green balls, and get lots of different values (due to small measurement errors) all centred around a mean value. You then measure the masses of a lot of blue balls, and get another distribution, this time centred around a mean value that is slightly larger. You want to know whether the balls are actually the same weight and the difference in mean masses is due to unavoidable random measurement errors (the null hypothesis), or because blue balls are genuinely heavier than green ones.
If the distributions are normally distributed, it is common to use a Student’s T test to answer this question. If the variations about the mean are due to myriad random physical errors, then because of the Central Limit Theorem, it will generally be the case that the distributions will be normal. However, there are many situations where this is not true.
Example use cases
An example of this might be a situation where Alice and Bob are trying to determine if they have the same size feet by comparing the sizes of various pairs of shoes that they own. These will certainly not be normally distributed, since shoe sizes are not continuous can not be negative.
An even trickier situation might be a situation where Alice and Bob are trying to determine if they have the same taste in films by comparing the ratings that they gave to different horror films, choosing from a rating of Terrible, Very Bad, Bad, Average, Good, Very Good, or Excellent. Again, these will not be normal due to the finite and discrete set of options. But now, the set of options is not even numerical! We don’t know whether the difference in quality between Excellent and Very Good is the same as the difference between Very Bad and Terrible. All we know is the order of the options, from worst to best. In fact, I analysed a similar case in my investigation of my friend’s diary.
In general, the Mann-Whitney U test is used when we have two independent samples, and we want to compare whether the median of one is greater than the median of the other by a statistically significant amount. The only strict requirement is that, for any two data points, $x$ and $y$, we can say whether $x<y$, $x>y$, or $x=y$.
The U statistic
The test centres around a statistic of the data, known as $U$. This is calculated as follows:
- Suppose we have $n=n_G + n_B$ data points drawn from two sets, which we call green and blue. Take all of these together and put them in order, from smallest to largest.
- Assign a rank to each point. The first point gets rank 1, the second point gets rank 2, all the way up to rank $n $.
- If any subset of data points are tied in rank, then assign all of them the median of the ranks that subset would have if they were different. So if we have 5 points that are all tied for first place, we assign them all rank of 1+(5-1)/2 = 3. The next point would then have rank 6.
- Calculate $R_G $ and $R_B$, which are the sums of the ranks of the green points and blue points respectively.
- Calculate $U_G = R_G - \frac{1}{2}n_G\left(n_G+1\right)$ and $U_B$.
- Let $U = \text{min}\left(U_G, U_B\right)$.
The distribution of this statistic under the null hypothesis is known. We can therefore check whether it takes on an extreme value to determine how likely it is that our distributions came from the null hypothesis.
Checking for statistical significance
Let’s take 100 green balls and 100 blue balls, and randomly and uniformly distribute their masses over the range 1 g → 100 g. Since these are drawn from the same distribution, the null hypothesis ($H_0$) is true in this case. Below we show in blue the distribution of $U$ values that results over many versions of these samples.
We also show in green the $U$ value that is found when we create a distribution where the median blue ball is 15 g heavier than the median green ball ($H_1$)
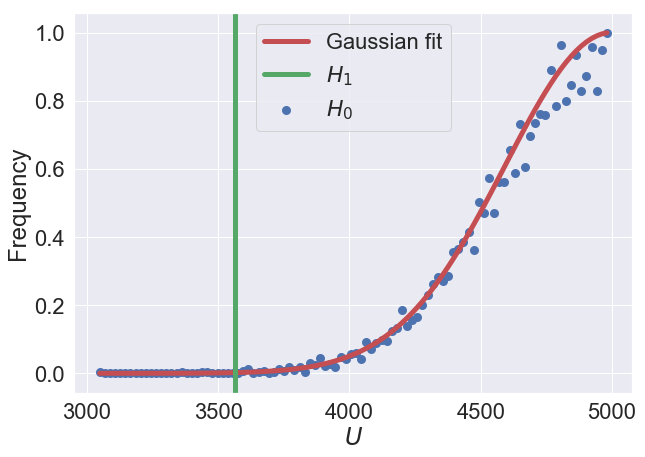
We can see that $U$ tends to form a normal-like distribution, although one-sided due to the fact that we take the minimum of $U_G$ and $U_B$ (we could alternatively not take the minimum and apply a two-tailed test). In fact we can prove that as the number of green and blue balls tends to infinity, the distribution of $U$ is exactly normal (but we won’t prove it because it is really complicated - if you’re interested, the paper is linked here).
When we have over 8 points in each sample, we can approximate the $U$ distribution by a normal distribution with mean $\mu=n_Gn_B/2$ and standard deviation $\sigma=\sqrt{n_Gn_B(n_G+n_B+1)/12}$ (not taking ties into account).
From here we can easily calculate a $p$-value; the probability that the given $U$ value arose from the null hypothesis. In the figure above, the case where the blue balls were 15 g heavier than the green balls gave rise to a very small $U$ value. This gives a $p$-value of 0.0002, so is very unlikely to be due to random chance.
Pros, cons, and cautions
When using a $p$-value, we always need to be mindful of over-interpretting the result. The probability that $H_0$ is false is not the same as the probability of $H_1$ being true. We should generally fix our alternative hypothesis. Say we think that blue balls are 10 g heavier than green balls. Let this alternative hypothesis be $\tilde{H}_1$. Suppose the $p$-value of the data arising from $H_0$ is 0.04, but the $p$-value of it arising from $\tilde{H}_1$ is 0.02. Then in this case, we cannot reject the null hypothesis, since the alternative is even more unlikely! We must simply accept that in this chaotic world, sometimes unlikely things can happen (and often do)!
The Mann-Whitney U test is very useful when we have data that can be compared in an ordinal way ($a<b$) but not in a numerical way ($a=b+\delta$). It is also useful when we have no information about the shape of our distribution, or cannot easily transform it to a normal form.
However, when the data are normal, then the Student’s T test is more efficient (requires less data for a conclusion). Also, when sample sizes are equal, the T test is more powerful than the U test, even when variances are unequal (a more powerful test is more likely to correctly reject $H_0$).
Importantly, the U test also does not check for differences in the mean values of the samples. If we want to check for this when we have non-normal data, we would need to use other non-parametric tests such as the Wilcoxon signed-rank test.
Overall, the Mann-Whitney U test is a super useful tool, and one that all data scientists should be aware of!

